Alexander Macfarlane
| Alexander Macfarlane | |
|---|---|
Alexander Macfarlane (1851 — 1913)
|
|
| Born | April 21, 1851 Blairgowrie, Scotland |
| Died | August 28, 1913 |
| Residence | Chatham, Ontario, Canada |
| Nationality | Scottish |
| Fields | Logic Physics Mathematics |
| Institutions | University of Texas Lehigh University |
| Alma mater | University of Edinburgh |
| Doctoral advisor | Peter Guthrie Tait |
| Known for | Scientific biographies Algebra of Physics |
| Influences | William Rowan Hamilton William Kingdon Clifford Arthur Cayley |
| Influenced | G. W. Pierce Quaternion Society |
Alexander Macfarlane FRSE (April 21, 1851 – August 28, 1913) was a Scottish logician, physicist, and mathematician.
Macfarlane was born in Blairgowrie, Scotland and studied at the University of Edinburgh. His doctoral thesis, on the conditions governing the electric spark, was subsequently published in the Transactions of the Royal Society of Edinburgh. It brought him to the notice of James Clerk Maxwell, and in 1878 Macfarlane was elected a Fellow of the Royal Society of Edinburgh
During his life, Macfarlane played a prominent role in research and education. He taught at the universities of Edinburgh and St Andrews, was physics professor at the University of Texas (1885 – 1894),[1] professor of Advanced Electricity, and later of mathematical physics, at Lehigh University. MacFarlane was the secretary of the Quaternion Society and compiler of its publications.
Macfarlane was also the author of a popular 1916 collection of mathematical biographies (Ten British Mathematicians), a similar work on physicists (Lectures on Ten British Physicists of the Nineteenth Century, 1919), and he compiled a bibliography on quaternions in 1904. Macfarlane was caught up in the revolution in geometry during his lifetime,[2] in particular through the influence of G. B. Halsted who was mathematics professor at the University of Texas. Macfarlane originated an Algebra of Physics, which was his adaptation of quaternions to physical science. His first publication on Space Analysis preceded the presentation of Minkowski Space by seventeen years.[3]
Macfarlane actively participated in several International Congresses of Mathematicians including the primordial meeting in Chicago, 1893, and the Paris meeting of 1900 where he spoke on "Application of space analysis to curvilinear coordinates".
Macfarlane retired to Chatham, Ontario, where he died in 1913.
Space analysis
Alexander Macfarlane stylized his work as "Space Analysis". In 1894 he published his five earlier papers and a book review of Alexander MacAulay’s Utility of Quaternions in Physics. This collection is now available on-line.[4] Page numbers are carried from previous publications, and the reader is presumed familiar with quaternions. The first paper is "Principles of the Algebra of Physics" where he first proposes the hyperbolic quaternion algebra, since "a student of physics finds a difficulty in principle of quaternions which makes the square of a vector negative." The second paper is "The Imaginary of the Algebra". Here he introduces the hyperbolic versor as the hyperbolic quaternion corresponding to the versor of Hamilton. The presentation is encumbered by the notation
Later he conformed to the notation exp(A α) used by Euler and Sophus Lie. The expression 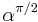 is meant to emphasize that α is a right versor, where π/2 is the measure of a right angle in radians. The π/2 in the exponent is, in fact, superfluous.
is meant to emphasize that α is a right versor, where π/2 is the measure of a right angle in radians. The π/2 in the exponent is, in fact, superfluous.
Papers three and four are "Fundamental Theorems of Analysis Generalized for Space" and "On the definition of the Trigonometric Functions", which he had presented the previous year in Chicago at the Congress of Mathematicians held in connection with the World's Columbian Exhibition. He follows George Salmon in exhibiting the hyperbolic angle, argument of hyperbolic functions. The fifth paper is "Elliptic and Hyperbolic Analysis" which considers the spherical law of cosines as the fundamental theorem of the sphere, and proceeds to analogues for the ellipsoid of revolution, general ellipsoid, and equilateral hyperboloids of one and two sheets, where he provides the hyperbolic law of cosines.
In 1900 Alexander published "Hyperbolic Quaternions"[5] with the Royal Society in Edinburgh, and included a sheet of nine figures, two of which display conjugate hyperbolas. Having been stung in the Great Vector Debate over the non-associativity of his Algebra of Physics, he restored associativity by reverting to biquaternions, an algebra used by students of Hamilton since 1853.
Works
- Macfarlane, Alexander (1916). Lectures on Ten British Mathematicians of the Nineteenth Century. New York: John Wiley and Sons. http://books.google.com/books?id=qWQSAAAAIAAJ&pg=PA34&dq=william+rowan+hamilton#PPP14,M2.
- Macfarlane, Alexander (1919). Lectures on Ten British Physicists of the Nineteenth Century. New York: John Wiley and Sons. http://www.archive.org/details/lecturesontenbri00macfrich.
- Works by Alexander Macfarlane at Project Gutenberg
Notes and references
- ^ See the Macfarlane papers at the University of Texas.
- ^ 1830–1930: A Century of Geometry, L Boi, D. Flament, JM Salanskis editors, Lecture Notes in Physics #402, Springer-Verlag ISBN 3540554084
- ^ A. Macfarlane (1891) "Principles of the Algebra of Physics", Proceedings of the American Association for the Advancement of Science 40:65-117. It was 1908 when Hermann Minkowski proposed his spacetime.
- ^ A. Macfarlane (1894) Papers on Space Analysis, B. Westerman, New York, weblink from archive.org
- ^ Macfarlane (1900) "Hyperbolic Quaternions" Proceedings of the Royal Society at Edinburgh, 1899-1900 session, pp. 169–181
- Colaw, J. M. (1895). "Alexander Macfarlane, M.A., D. Sc., LL.D". The American Mathematical Monthly 2: 1–4. doi:10.2307/2971573.
- Robert de Boer (2009) Biography of Alexander Macfarlane from WebCite.
- Electric Scotland historical biography
- Knott, Cargill Gilston, Alexander Macfarlane (obituary), Nature, 25 September 1913.
- Macfarlane papers at the University of Texas